개요
기본 이진트리와 레드블랙트리를 구현해보고, 시각화하여 확인할 수 있도록 합니다.
다른 컨테이너들과 성능을 비교해보고 게임 서버에서의 사용처를 분석합니다.
레드블랙트리 구현
이진탐색트리의 한계
이진탐색트리는 구현이 간편하지만, 다음 극명한 한계점들을 가지고 있습니다.
노드가 한쪽으로 쏠려서 관리될 수 있기에, 성능은 최악의 경우에 O(N)의 시간을 소모합니다.
이러한 경우 선형 탐색과 다를 바가 없기에, 기본 이진탐색트리를 사용하는 경우는 드뭅니다.
균형잡기 (밸런싱)과 회전
이러한 이진탐색트리의 한계를 극복하기 위해,
자체적으로 노드들의 높이를 맞출 수 있는 자가균형트리에서는 회전을 통해 노드간 밸런스를 맞춥니다.
코드와 주석이 문서 뒤에 위치합니다
레드블랙트리의 특징
레드블랙트리는 다음 네 가지의 특징을 가지고 있습니다.
- 모든 노드는 레드 혹은 블랙의 색상을 진다.
- 레드 노드의 자식 노드는 언제나 블랙이다.
- 임의의 한 노드에서 널 리프 노드까지의 모든 경로에는 같은 수의 블랙 노드가 있어야 한다.
- 루트 노드와 리프 노드는 블랙이다.
인터페이스
void Insert(int key, T item);
void Remove(int key);
bool Find(int key, T *outValue);
void Clear();
void PrintInOrder(char *outBuffer = nullptr);
void RotateRight(int key);
void RotateLeft(int key);기본적으로 위의 일곱 가지의 기능을 제공하도록 구현하였으며,
추가적인 검증 절차 및 편의를 위해 다음 기능을 제공하도록 하였습니다.
// 트리에 로직상 존재해야 할 노드 개수를 리턴합니다.
int GetItemCount();
// 루트부터 탐색하며 실제 카운팅된 노드 개수를 리턴합니다.
int GetItemCountCheck();
// 마지막으로 추가된 노드의 키를 리턴합니다.
int GetItemLastAddedKey();
// 마지막으로 추가된 노드의 값을 리턴합니다.
bool GetItemLastAddedValue(T *outValue);
// 레드블랙트리가 규칙을 준수하고 있는지 검사합니다.
int IsBrokenTree();
// 루트부터 말단 노드 경로에서의 블랙 노드 개수를 리턴합니다.
int GetRouteBlackNodeCount();삽입과 밸런싱
이진탐색트리와 동일하게, 삽입할 노드의 위치까지 탐색 후, 노드를 삽입합니다.
이 때, 삽입하는 노드의 색상은 레드입니다. (블랙이라면 밸런스 작업이 불가피해집니다.)
이후, 부모가 레드였다면 삽입 후 밸런스 작업에 들어갑니다.
코드와 주석이 문서 뒤에 위치합니다
삭제와 밸런싱
이진탐색트리와 동일한 삭제 로직을 가집니다. 자식을 가지지 않는 말단 노드였다면 바로 삭제해도 상관이 없지만, 자식을 하나 가지고 있다면 부모와 자식을 연결해주며, 자식을 둘 가지고 있다면 말단 노드들 중 가장 자신과 값이 가까운 노드를 찾아, 해당 노드를 대신 삭제합니다.
이후, 삭제한 노드 (자식이 둘이었던 경우 실제 삭제된 노드)가 만일 레드였다면, 삭제되어도 밸런스에 문제가 없습니다. 따라서 해당 노드가 블랙이었을 경우에 밸런스 작업에 들어갑니다.
코드와 주석이 문서 뒤에 위치합니다
레드블랙트리 시각화
레드블랙트리는 색상을 가지고 이것이 중요한 규칙과 연관되기에 시각화하여 눈으로 확인할만한 가치가 있습니다.
따라서 윈도우 응용어플리케이션에 GDI를 사용하여 레드블랙트리를 시각화하였습니다.

코드와 주석이 문서 뒤에 위치합니다
레드블랙트리의 검증
개발 과정에서 모든 일련의 동작 이후, 레드블랙트리의 대전제를 어기지 않는지 검증이 필요합니다. 첫 째로, 모든 말단 노드로의 경로에서 블랙 노드의 개수가 모두 일치하는지 검사해야 합니다. 또한, 탐색중 만일 부모 노드와 현재 노드 모두 레드 색상이라면 규칙이 깨진 것으로 판별해야 합니다.
추가적으로, 회전이나 일련의 동작 중 노드 간 연결이 정상적으로 되지 않았을 수 있기에, 로직 상 삽입된 노드 개수와 삭제된 노드 개수를 저장해 놓고, 이를 실제 root부터 탐색해본 모든 노드 개수와 비교해 보면 더욱 확실한 검증을 이룰 수 있습니다.
또한, 레드블랙트리 자체의 검증이 아닌, 동작이 확실한 std::map 자료구조에도 동일한 작업을 진행하며, 모든 절차마다 레드블랙트리에서의 중위순회한 결과와 std::map에서 중위순회한 결과를 비교하여 자료구조 구현상의 이상을 확인할 수 있습니다.
코드와 주석이 문서 뒤에 위치합니다
레드블랙트리와 비교군 분석
레드블랙트리는 이진탐색트리보다 밸런스를 잡는 추가적인 연산이 필요하지만, 이를 통해 얻는 말단 노드까지의 높이 감소 덕분에 요소 개수가 늘어날수록 이진탐색트리와는 극명한 성능차이를 보여줍니다. 따라서, 첫번째 비교군은 기본적인 이진탐색트리로 잡았습니다.
이진탐색트리만큼 단순한 구조를 가진 연결리스트 자료구조를 두번째 비교군으로 산정하였고, 트리와는 다른 성격을 가진, 해시테이블 기반의 std::unordered_map 을 세번째 비교군으로 선정하여, 성능 비교와 복잡도를 같이 살펴보도록 하였습니다.
또한, C++ STL 에서도 std::map 자료구조가 레드블랙트리를 기반으로 하고 있기에, 동일한 성격을 보여주는지 확인하기 위해 이를 마지막 비교군으로 선정하였습니다.
시간복잡도 비교
| 종류 | 삽입 | 삽입(최악) | 검색 | 검색(최악) | 삭제 | 삭제(최악) |
|---|---|---|---|---|---|---|
| 이진탐색트리 | O(log N) | O(N) | O(log N) | O(N) | O(log N) | O(N) |
| 링크드리스트 | O(1) | O(1) | O(N) | O(N) | O(N) | O(N) |
| 레드블랙트리 | O(log N) | O(log N) | O(log N) | O(log N) | O(log N) | O(log N) |
| 해시테이블 | O(1) | O(N) | O(1) | O(N) | O(1) | O(N) |
링크드리스트의 경우 특정 값을 삭제하는 것을 기준으로 한 복잡도입니다.
이진탐색트리의 경우 최선의 경우 레드블랙트리와 동일한 시간복잡도를 가집니다. (밸런스가 완벽히 맞추어진 경우, AVL과 동일한 시간복잡도) 하지만, 이러한 상황은 쉽게 만들어지지 않으며, 점차 한쪽으로 쏠린 자료구조가 되어 O(N)에 수렴되게 됩니다.
링크드리스트를 이용하여 현재 목적으로 하는 인터페이스대로 구현한 경우, 삽입은 요소 개수와 상관없이 O(1) 시간에 가능하지만, 검색과 삭제를 위해 head부터 탐색해나가야 하는, O(N)의 시간복잡도를 가집니다.
레드블랙트리의 경우 AVL보다는 덜하지만, 좌우 밸런스가 충분히 맞추어져 있기에 요소가 늘어나더라도 트리의 높이는 쉽게 늘어나지 않습니다. 따라서 O(log N)이라는 안정된 시간복잡도를 삽입, 검색, 삭제 모두에서 가집니다.
해시테이블의 경우 해시 함수의 분포도에 따라 성능이 극명하게 갈리겠지만, 이론상 삽입과 검색, 삭제 모두 O(1)의 시간복잡도로 바로 요소에 접근이 가능합니다. 하지만, 이진탐색트리와 마찬가지로 데이터가 만일 한쪽에 (한 버킷에) 쏠리게 된다면 점차 O(N)의 시간복잡도를 가지게 될 수 있습니다. 이는 버킷 내부의 동일 키 자료들은 레드블랙트리로 관리하는 등 복합적인 자료구조를 통해 개선할 수 있을 것입니다.
비교군별 실제 성능 확인
실제 데이터셋을 가지고 성능을 확인해 보았습니다.
삽입 로직 : 0~1000사이의 값을 가진 랜덤 순서의 512개의 값을 삽입합니다. (중복 제외)
검색 로직 : 데이터셋에 들어간 값 중 랜덤 순서로 512개의 값을 검색합니다.
삭제 로직 : 0부터 1000순서로 만일 자료구조에 포함된 값이라면 삭제를 시도합니다.
다음 결과는 위의 로직에 맞추어 512개의 요소를 삽입 후, 512개의 요소를 검색 후, 512개를 삭제하는 작업을 1024회 반복한 총 소요 시간입니다
| 종류 | 삽입 속도 (1024회) | 검색 속도 (1024회) | 삭제 속도 (1024회) |
|---|---|---|---|
| 이진탐색트리 | 0.135초 | 0.089초 | 0.151초 |
| 레드블랙트리 | 0.195초 | 0.048초 | 0.153초 |
| std::list | 0.290초 | 19.91초 | 10.39초 |
| std::unordered_map | 0.467초 | 0.222초 | 0.226초 |
| std::map | 0.608초 | 0.357초 | 0.535초 |
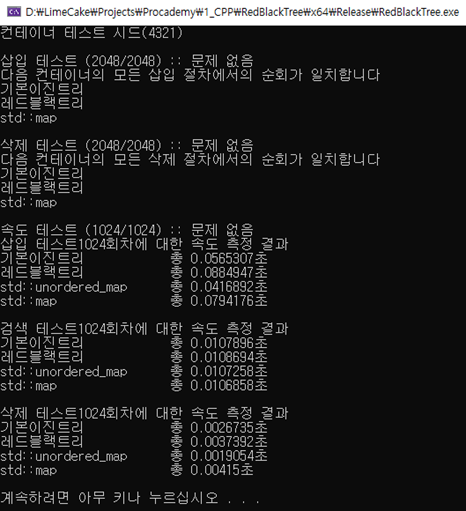
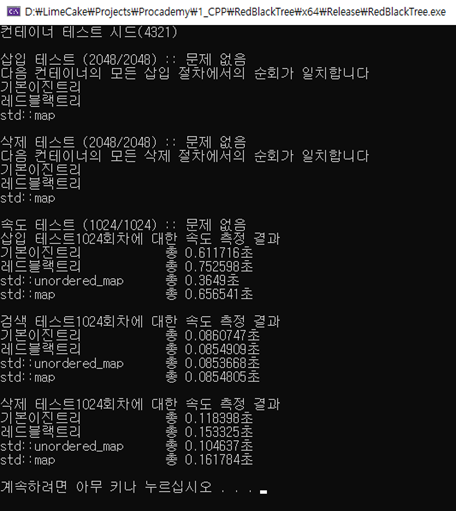
이진탐색트리와 비교하여 레드블랙트리가 삽입 비용이 더 큰 것은, 밸런스 작업 비용으로 볼 수 있습니다. 이는 자료구조가 가지는 요소 수가 늘어날수록 레드블랙트리에게 성능상 이점을 줄 것입니다. 테스트 결과에서도 512개 요소 테스트에서의 삽입 성능 차이보다 4096개 요소 테스트일 때 간극이 좁혀진 것을 볼 수 있습니다.
연결리스트가 검색과 삭제에O(N) 복잡도를 가짐으로서 확연히 가장 느린 성능을 보여주었습니다. 이는 기존 연결리스트의 구현 주 목적인 head와 tail에서의 작업을 배제하고, 특정 값을 찾아 사용하는 자료구조로 사용하였기에 이러한 성능을 보였습니다. 따라서 연결리스트 자료구조는 스택이나 큐와 같이 head와 tail기준으로 작업하는 자료구조의 구현에 사용해야 합니다.
해시테이블 기반의 unordered map은 map에 비해 더욱 좋은 성능을 보여주었습니다. 이는 해시테이블이 가진 O(1)의 시간복잡도 접근 가능성 덕분이며, 성능이 필요한 경우, map의 기능이 필요한 경우가 아니라면 해시테이블 기반인 unordered map 사용이 더욱 좋은 선택입니다.
결론
레드블랙트리는 이진탐색트리의 단점을 해소하였고, AVL 트리보다는 조금 더 밸런스에 여유를 둠으로서 삽입과 삭제, 검색 모두 안정적인 성능을 보여주는 컨테이너입니다. 또한, 이는 이진탐색트리 기반이기에 중위순회를 통해 정렬된 데이터셋을 찾을 수 있다는 장점 또한 있습니다.
레드블랙트리의 다음 말단 노드들을 서로 포인터로 참조한다면, iterator를 이용하여 자료구조 전체 데이터를 순회할 수 있게 개선할 수 있습니다. 이는 해시테이블 기반의 stl 자료구조인 unordered_map 의 이름에서도 알 수 있는, map 이 줄 수 있는 차별점입니다.
게임서버에서 이러한 컨테이너는 수많은 곳에 쓰일 수 있습니다. 길이가 정해져 있지 않은, 길이의 유동성이 큰 데이터셋이라면 배열로 관리하는 것보다 이러한 자료구조로 관리하는 것이 더욱 편리함을 줄 수 있지만, unordered_map과 map을 적지 적소에 쓸 줄 알아야 합니다.
std::unordered_map은 일반적으로 사용해도 좋을 정도의, 강력한 성능을 가진 컨테이너입니다. 만일 자료들을 정렬된 순서로 순회해야 하거나, 특정 바운더리의 데이터셋을 추출해서 작업해야 하는 경우에는 unordered_map 사용이 불가능합니다.
| std::unordered_map | std::map |
|---|---|
| 정렬된 데이터로 관리될 필요 없는 경우, 플레이어 세션리스트, 퀘스트 리스트 등 파일로 불러온 대량 데이터 | 해시함수로 분포를 고르게 할 수 없는 경우, 정렬된 순서로 순회해야 하는 경우, 특정 바운더리의 데이터를 다루는 경우 |
코드 모음
이진탐색트리에서의 회전
Node *_rotateRight(int key, Node *position)
{
if (position == nullptr || position == &_nilNode) return nullptr;
if (position->key > key)
{
_rotateRight(key, position->left);
return position;
} else if (position->key < key)
{
_rotateRight(key, position->right);
return position;
}
// 현재 노드가 회전해야 할 대상 노드
Node *parent = position->parent;
Node *left = position->left;
// 왼쪽 자식이 nilNode인 경우 회전시키지 않는다
if (left == &_nilNode) return position;
if (parent != nullptr)
{
// 부모가 존재하는 경우 부모의 자식 포인터 수정
if (parent->left == position)
{
parent->left = left;
} else
{
parent->right = left;
}
}
// 왼쪽 자식이 내 부모의 자식이 된다
left->parent = parent;
// 왼쪽 자식이 내 부모가 된다
position->parent = left;
// 왼쪽 자식의 오른쪽 자식을 내 왼쪽 자식으로 가져온다
position->left = left->right;
if (position->left != &_nilNode)
{
// 해당 자식의 부모를 나로 포인터 수정
position->left->parent = position;
}
// 왼쪽 자식의 오른쪽 자식이 내가 된다
left->right = position;
return left;
}
Node *_rotateLeft(int key, Node *position)
{
// ...우회전을 좌우 반전하여 동작한다
}레드블랙트리 삽입 후 밸런스 작업
void _balanceInsert(Node *position)
{
// ...부모와 조부모 포인터가 존재하는지 검사합니다
// ...부모의 색상이 레드가 아니라면 리턴합니다
Node *positionUncle = nullptr;
// ...삼촌 노드를 찾습니다.
if (positionUncle->color == RED)
{
// 삼촌 노드의 색상이 레드라면 규칙 1번
_balanceInsertCase1(position);
} else if (positionUncle->color == BLACK && position->parent->parent->left == position->parent)
{
// 삼촌 노드의 색상이 블랙이고, 부모가 조부모의 왼쪽 자식이라면 규칙 2번
_balanceInsertCase2(position);
} else if (positionUncle->color == BLACK && position->parent->parent->right == position->parent)
{
// 삼촌 노드의 색상이 블랙이고, 부모가 조부모의 오른쪽 자식이라면 규칙 3번
_balanceInsertCase3(position);
}
}
// 1. 삼촌이 레드인 경우
// 부모와 삼촌을 블랙으로 바꾸고, 할아버지를 레드로 바꾼다.
// 이 작업을 상위로 올라가며 반복한다.
void _balanceInsertCase1(Node *position)
{
Node *positionUncle = nullptr;
if (position->parent->parent->left == position->parent) positionUncle = position->parent->parent->right;
if (position->parent->parent->right == position->parent) positionUncle = position->parent->parent->left;
position->parent->color = BLACK;
positionUncle->color = BLACK;
position->parent->parent->color = RED;
_balanceInsert(position->parent->parent);
}
// 2. 삼촌이 블랙인 경우, 부모가 왼쪽 노드였을 경우
void _balanceInsertCase2(Node *position)
{
Node *currentPosition = position;
if (currentPosition->parent->right == currentPosition)
{
// 부모의 오른쪽 자식일 경우
// 한쪽으로 몰리게끔 우선 회전한다
// 부모를 왼쪽 회전
_rotateLeft(currentPosition->parent->key, currentPosition->parent);
// 포커스는 말단 노드인, 회전되어 말단이 된 옛 부모, 왼쪽 노드
currentPosition = currentPosition->left;
}
// 부모의 왼쪽 자식일 경우
// 조부모를 레드로, 부모를 블랙으로
currentPosition->parent->parent->color = RED;
currentPosition->parent->color = BLACK;
// 조부모를 오른쪽 회전
RotateRight(currentPosition->parent->parent->key);
}
// 3. 삼촌이 블랙인 경우, 부모가 오른쪽 노드였을 경우
void _balanceInsertCase3(Node *position)
{
// ...2번 조건을 좌우대칭한 동작을 진행합니다.
}모든 삽입 작업 이후에는 루트를 블랙으로 색상을 덮어씌웁니다.
레드블랙트리 삭제 후 밸런스 작업
void _balanceRemove(Node *target)
{
// ...대상 노드가 레드라면 리턴합니다.
// ...대상 노드가 루트라면 리턴합니다.
if (target == target->parent->left)
{
// 부모의 왼쪽 자식일 경우
_balanceRemoveCase1(target);
} else // if (target == target->parent->right)
{
// 부모의 오른쪽 자식일 경우
_balanceRemoveCase2(target);
}
}
// 1. 내가 부모의 왼쪽 자식일 경우
void _balanceRemoveCase1(Node *target)
{
Node *sibling = target->parent->right;
if (sibling->color == RED)
{
sibling->color = BLACK;
target->parent->color = RED;
RotateLeft(target->parent->key);
_balanceRemove(target);
return;
}
// 형제의 모든 자식이 블랙이었을 경우, 회전을 통해서 해결이 불가능
// 따라서 형제를 레드로 만들어 나와 형제간 밸런스를 맞추고, 부모부터 위로 리밸런스
if (sibling->left->color == BLACK && sibling->right->color == BLACK)
{
sibling->color = RED;
_balanceRemove(target->parent);
return;
}
if (sibling->right->color == BLACK)
{
// 형제의 왼쪽이 레드, 오른쪽 자식이 블랙인 경우
// 회전을 통해 형제의 오른쪽이 레드인 경우로 바꾼다
sibling->left->color = BLACK;
sibling->color = RED;
RotateRight(sibling->key);
_balanceRemove(target);
} else // sibling->right->color == RED
{
// 형제의 오른쪽 자식이 레드인 경우
// 형제의 자식 색을 블랙으로, 부모도 블랙으로 바꾸고 부모를 회전
// 이로서 내 쪽으로 블랙을 하나 가져올 수 있기에, 삭제 전과 블랙 밸런스 동일
sibling->color = target->parent->color;
target->parent->color = BLACK;
sibling->right->color = BLACK;
RotateLeft(target->parent->key);
}
}
// 2. 내가 부모의 오른쪽 자식일 경우
void _balanceRemoveCase2(Node *target)
{
// ...1번 조건을 좌우대칭한 동작을 진행합니다.
}레드블랙트리 시각화 코드
VOID _drawTree(Node *current, HDC memoryDC, INT32 top, INT32 left, INT32 right)
{
if (current == nullptr) return;
if (current == &_nilNode) return;
// 그릴 포지션을 잡습니다
INT32 drawNodePositionXStart = (left + right) / 2 - 15;
INT32 drawNodePositionXEnd = (left + right) / 2 + 15;
INT32 drawNodePositionYStart = top;
INT32 drawNodePositionYEnd = top + 30;
// 키값을 문자열로 변환합니다
WCHAR buffer[8] = { 0, };
_snwprintf_s(buffer, 10, L"%4d", current->key);
HBRUSH hbr = NULL;
if (current->color == BLACK) hbr = CreateSolidBrush(RGB(0, 0, 0));
if (current->color == RED) hbr = CreateSolidBrush(RGB(255, 0, 0));
// 색상에 맞추어 원을 그립니다
HBRUSH hbrOld = static_cast<HBRUSH>(SelectObject(memoryDC, hbr));
Ellipse(memoryDC, drawNodePositionXStart, drawNodePositionYStart, drawNodePositionXEnd, drawNodePositionYEnd);
SelectObject(memoryDC, hbrOld);
DeleteObject(hbr);
// 원 안에 문자열로 변환한 키값을 표시합니다
SetTextColor(memoryDC, RGB(255, 255, 255));
SetBkMode(memoryDC, TRANSPARENT);
TextOutW(memoryDC, drawNodePositionXStart - 1, drawNodePositionYStart + 5, buffer, wcslen(buffer));
SetTextColor(memoryDC, RGB(0, 0, 0));
if (current->left != &_nilNode)
{
// 왼쪽 자식을 그립니다
INT32 drawLeftChildLeft = left;
INT32 drawLeftChildRight = (left + right) / 2;
INT32 drawLeftChildTop = top + 50;
_drawTree(current->left, memoryDC, drawLeftChildTop, drawLeftChildLeft, drawLeftChildRight);
HPEN hPen = CreatePen(PS_SOLID, 2, BLACKNESS);
HPEN hPenOld = static_cast<HPEN>(SelectObject(memoryDC, hPen));
MoveToEx(memoryDC, (drawNodePositionXStart + drawNodePositionXEnd) / 2, drawNodePositionYEnd, nullptr);
LineTo(memoryDC, (drawLeftChildLeft + drawLeftChildRight) / 2, drawLeftChildTop);
SelectObject(memoryDC, hPenOld);
DeleteObject(hPen);
}
if (current->right != &_nilNode)
{
// ...오른쪽 자식을 그립니다
}
}레드블랙트리 검증 코드
public : int IsBrokenTree()
{
_checkBlackNodeCount = 0;
return _isBrokenTree(_root);
}
private : int _isBrokenTree(Node *current)
{
// 말단 노드까지 탐색합니다
if (current == nullptr || current == &_nilNode) return 0;
// 탐색중 만일 부모 색상과 현재 노드 색상 모두 레드라면, 규칙이 깨졌습니다
if (current->parent != nullptr && current->parent->color == RED && current->color == RED)
{
return -1;
}
if (current->left != &_nilNode)
{
int result = _isBrokenTree(current->left);
if (result != 0) return result;
}
if (current->right != &_nilNode)
{
int result = _isBrokenTree(current->right);
if (result != 0) return result;
}
if (current->left == &_nilNode && current->right == &_nilNode)
{
// 말단 노드인 경우
Node *temp = current;
int blackNodeCount = 0;
while (temp != nullptr)
{
// 루트까지 탐색하며 블랙 개수를 카운트합니다
if (temp->color == BLACK) blackNodeCount++;
temp = temp->parent;
}
// 기존 저장된 블랙 개수가 있다면 비교하고, 없다면 초기화합니다.
if (_checkBlackNodeCount == 0) _checkBlackNodeCount = blackNodeCount;
if (_checkBlackNodeCount != 0 && _checkBlackNodeCount != blackNodeCount)
{
// 다른 말단 노드와 블랙 개수가 불일치합니다.
return -2;
}
}
return 0;
}레드블랙트리 자료구조 로직 검증 코드
// 삽입이 정상적인 로직으로 구현되었는지 테스트합니다
bool doInsertTest(int requiredTestCount)
{
insertTestCurrentCount = 0;
insertTestRequiredCount = requiredTestCount;
insertTestStatus = 1;
bool testResult = true;
BinarySearchTree *bst = new BinarySearchTree;
RedBlackTree<int> *rbt = new RedBlackTree<int>;
ListComparator *compareList = new ListComparator;
OrderedMapComparator *compareMap = new OrderedMapComparator;
char buffer1[STR_OUTPUT_BUFFER_SIZE];
char buffer2[STR_OUTPUT_BUFFER_SIZE];
char buffer3[STR_OUTPUT_BUFFER_SIZE];
char buffer4[STR_OUTPUT_BUFFER_SIZE];
int randomKey = 0;
int randomValue = 0;
int outValue = 0;
while (true)
{
for (int i = 0; i < 36; i++)
{
memset(buffer1, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer2, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer3, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer4, 0, STR_OUTPUT_BUFFER_SIZE);
randomKey = rand() % 100;
randomValue = rand() % 100;
outValue = 0;
// 만일 이미 자료구조에 삽입된 값이라면 다른 값으로 다시 시도합니다
if (rbt->Find(randomKey, &outValue)) {
i--;
continue;
}
// 자료구조에 삽입합니다
bst->InsertItem(randomKey, randomValue);
rbt->Insert(randomKey, randomValue);
compareList->InsertItem(randomKey, randomValue);
compareMap->InsertItem(randomKey, randomValue);
// 버퍼에 문자열 형태로 자료를 중위순회한 결과를 출력합니다
bst->PrintInOrder(buffer1);
rbt->PrintInOrder(buffer2);
compareList->PrintSortedOrder(buffer3);
compareMap->PrintSortedOrder(buffer4);
// 자료구조마다 출력한 버퍼들이 모두 같은지 비교합니다
bool isResultSame = memcmp(buffer1, buffer2, STR_OUTPUT_BUFFER_SIZE) == 0;
isResultSame = isResultSame && memcmp(buffer1, buffer3, STR_OUTPUT_BUFFER_SIZE) == 0;
isResultSame = isResultSame && memcmp(buffer1, buffer4, STR_OUTPUT_BUFFER_SIZE) == 0;
if (!isResultSame)
{
testResult = false;
break;
}
}
bst->Clear();
rbt->Clear();
compareList->Clear();
compareMap->Clear();
insertTestCurrentCount++;
if (insertTestCurrentCount >= insertTestRequiredCount || !testResult) break;
printCurrentStatus(true);
}
return testResult;
}
// 삭제가 정상적인 로직으로 구현되었는지 테스트합니다
bool doDeleteTest(int requiredTestCount)
{
deleteTestCurrentCount = 0;
deleteTestRequiredCount = requiredTestCount;
deleteTestStatus = 1;
bool testResult = true;
BinarySearchTree *bst = new BinarySearchTree;
RedBlackTree<int> *rbt = new RedBlackTree<int>;
ListComparator *compareList = new ListComparator;
OrderedMapComparator *compareMap = new OrderedMapComparator;
char buffer1[STR_OUTPUT_BUFFER_SIZE];
char buffer2[STR_OUTPUT_BUFFER_SIZE];
char buffer3[STR_OUTPUT_BUFFER_SIZE];
char buffer4[STR_OUTPUT_BUFFER_SIZE];
int randomKey = 0;
int randomValue = 0;
int outValue = 0;
while (true)
{
for (int i = 0; i < 36; i++)
{
// 삽입 로직은 위와 동일
}
for (int i = 0; i < 100; i++)
{
memset(buffer1, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer2, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer3, 0, STR_OUTPUT_BUFFER_SIZE);
memset(buffer4, 0, STR_OUTPUT_BUFFER_SIZE);
// 만일 자료구조에 없는 값이라면 다음 값으로 다시 시도합니다
if (!rbt->Find(i, nullptr)) {
continue;
}
// 자료구조에서 삭제합니다
bst->RemoveItem(i);
rbt->Remove(i);
compareList->RemoveItem(i);
compareMap->RemoveItem(i);
// 버퍼에 문자열 형태로 자료를 중위순회한 결과를 출력합니다
bst->PrintInOrder(buffer1);
rbt->PrintInOrder(buffer2);
compareList->PrintSortedOrder(buffer3);
compareMap->PrintSortedOrder(buffer4);
// 자료구조마다 출력한 버퍼들이 모두 같은지 비교합니다
bool isResultSame = memcmp(buffer1, buffer2, STR_OUTPUT_BUFFER_SIZE) == 0;
isResultSame = isResultSame && memcmp(buffer1, buffer3, STR_OUTPUT_BUFFER_SIZE) == 0;
isResultSame = isResultSame && memcmp(buffer1, buffer4, STR_OUTPUT_BUFFER_SIZE) == 0;
if (!isResultSame)
{
testResult = false;
break;
}
}
bst->Clear();
rbt->Clear();
compareList->Clear();
compareMap->Clear();
deleteTestCurrentCount++;
if (deleteTestCurrentCount >= deleteTestRequiredCount || !testResult) break;
printCurrentStatus(true);
}
return testResult;
}'연구한 이야기 > 깊게 공부해보기' 카테고리의 다른 글
| IOCP 서버 코어 개발하기 (2) | 2023.06.06 |
|---|---|
| 패킷 직렬화버퍼 (0) | 2023.05.02 |
| 메모리풀과 프리리스트 (0) | 2023.05.02 |
| TCP와 링버퍼 (0) | 2023.05.02 |
| 더 빠른 길찾기 (0) | 2023.05.02 |
